Cosine Similarity vs. Euclidean Distance: Vector Search Explained

In previous posts, we explored how to create embeddings using special large language models. Now, we need to discuss how we actually use those embeddings to perform semantic similarity searching.

We have discussed the technique of searching a database full of embeddings by plotting a search query onto a graph and then looking for the closest vectors around it. But how do you actually do that? How do you mathematically determine which vectors are the "closest" to your search query?

There are two common ways you can find these search results in a vector database. They are called Cosine Similarity and Euclidean Distance.

A quick warning: there is going to be a little bit of math in this post, but we will keep it grounded in visual examples.

Visualizing Vector Space

For simplicity, let's imagine we have vectors in a two-dimensional space. Let's go back to an example where we measure "cuteness" on the Y-axis and "dangerousness" on the X-axis. We have various words plotted onto this two-dimensional vector space based on these attributes.

Let's say we want to pick out one of these items, specifically "Cat," and find the vectors that are closest to it.

Euclidean Distance

The simplest method to visualize is called Euclidean distance. This is likely how you naturally think about distance in the physical world. You take the item you want to measure from, you simply draw a straight line to the closest item, and then you work out how long that line is.

For the item "Cat," if we draw a line to "Rabbit" and calculate the length of that line, and then draw a line to "Mouse" and calculate that length, we can compare them. We can also draw a line down to "Lawyer" and calculate that.

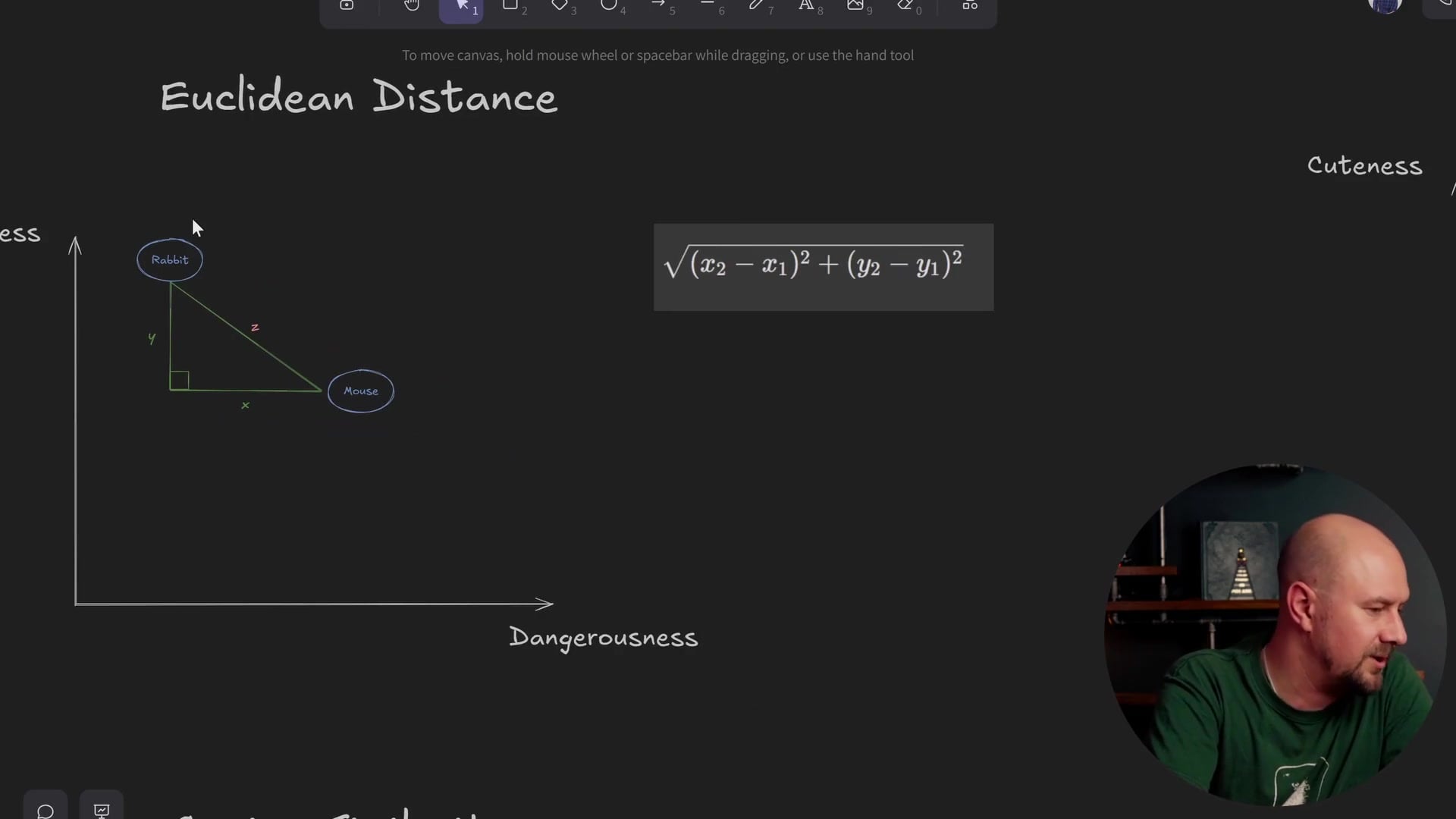
By looking at the lengths of these lines, we can say that the shorter the line is, the more similar the item is to the vector we are querying.

The Math Behind Euclidean Distance

You can calculate the lengths of these lines using standard trigonometry. If you recall the Pythagorean theorem, you basically draw a right-angled triangle between the two points. While this is simple in a two-dimensional space, this concept scales to multiple dimensions as well, and the formula remains largely the same.

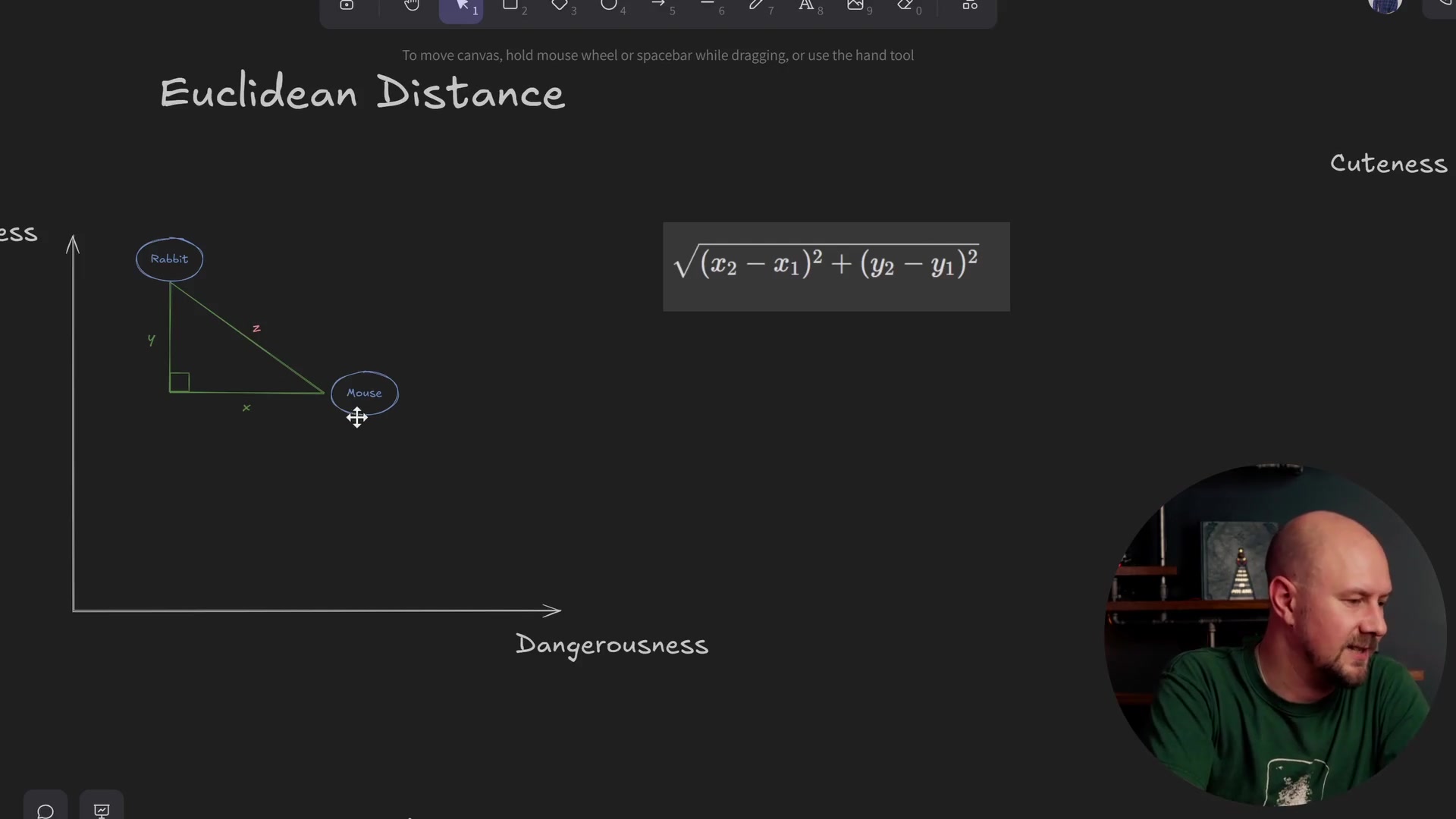
In this formula, \(z\) represents the length of the line we want to calculate. You calculate the \(z\) distance based on the differences in \(y\) and \(x\) coordinates.

For example:

• If "Mouse" has an X coordinate of 5 and "Rabbit" has an X coordinate of 2, the difference (\(x\)) is 3.
• You calculate the difference for \(y\) in the same way.
• Feed these values into the formula to get the value for \(z\).

This is one valid way of calculating the closest items to a certain search query: simply calculating the distance in multi-dimensional Euclidean space.

Cosine Similarity

However, there is another approach called Cosine Similarity.

As mentioned in previous posts, there are two ways to describe a vector. You can describe it by its coordinates (using X and Y), or you can think of it as a line that originates from the center (the origin) and has a specific angle and length.

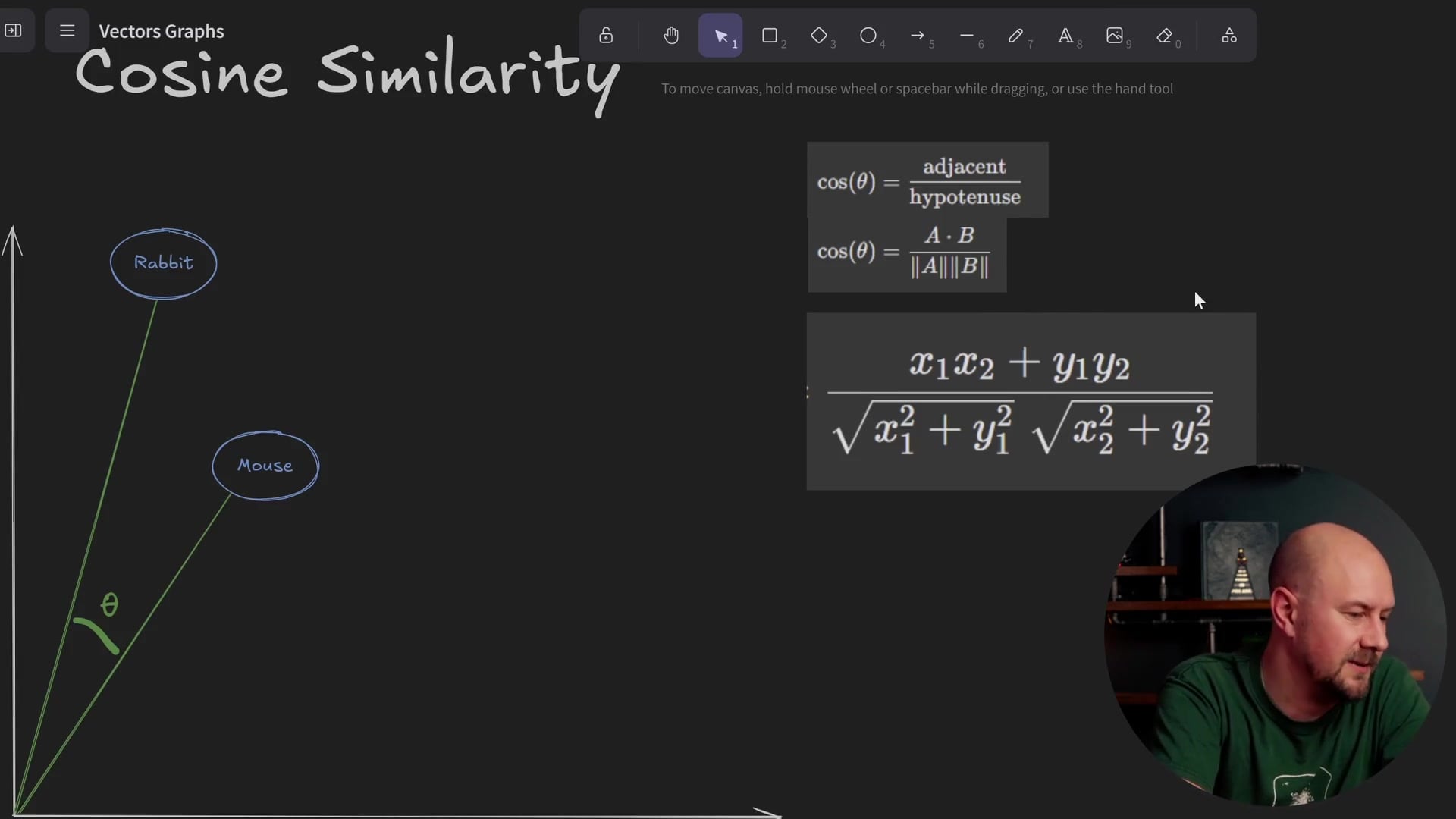
Cosine similarity utilizes this second property of vectors. It relies on the fact that vectors have a length and an angle. Instead of comparing the absolute distance between points (the orange lines in our previous example), it compares the difference in the angle between the vectors.

The Math Behind Cosine Similarity

We compare the angle of incidence from the origin. To do this, we use trigonometry to calculate the cosine of the angle.

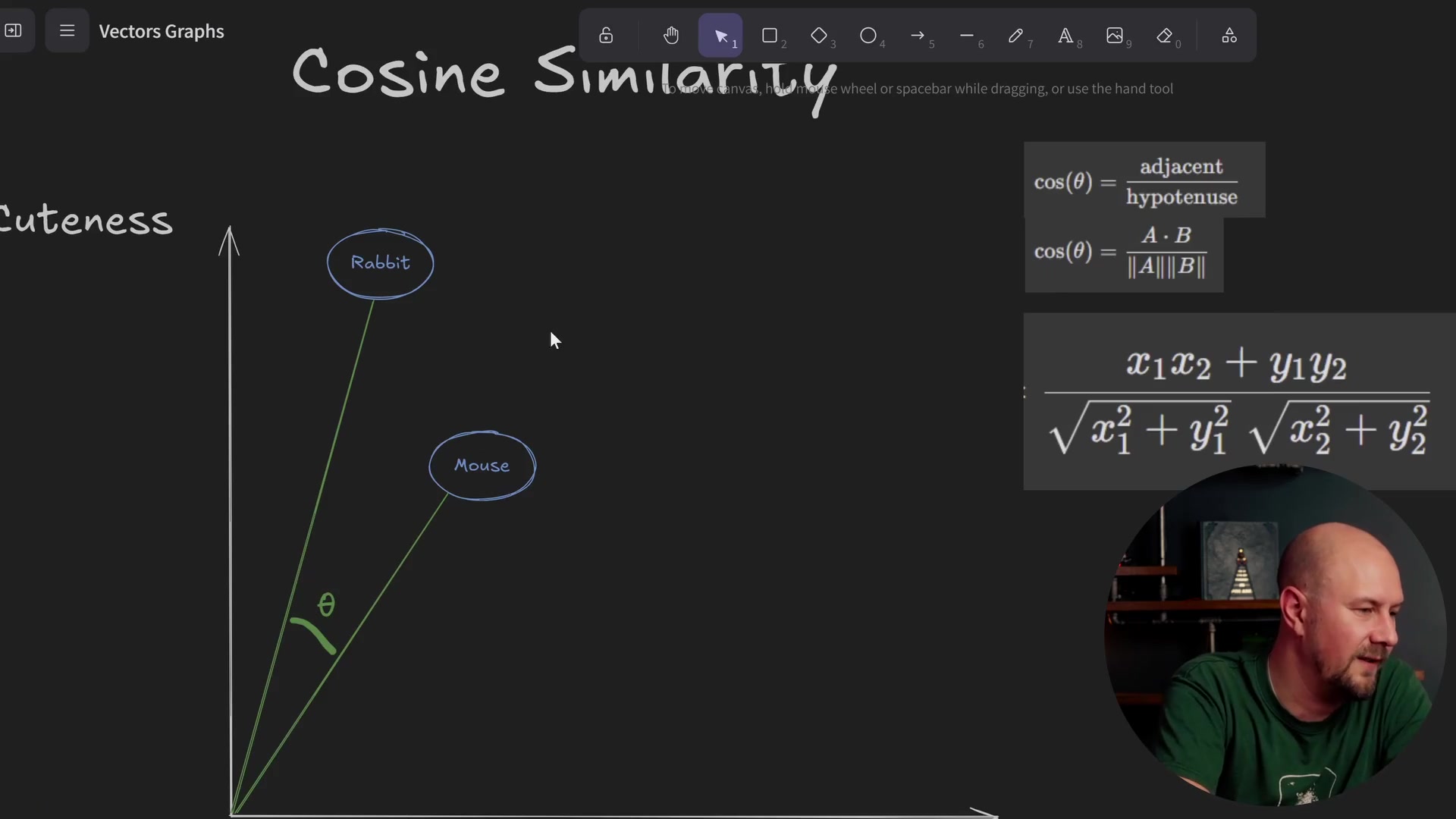
The formula calculates the cosine of the angle (\(\theta\)) between the two vectors. By calculating this angle between your query vector and all other vectors in your graph, you can determine that vectors with similar angles are "similar" vectors.

Comparing the Results

These are two distinct approaches that will give you two different values. Both are useful, and the one you pick really depends on your data, how you are storing it, and how you want your search to function. However, looking at an example demonstrates why you might pick one over the other for semantic search.

Let's look at our "cuteness vs. dangerousness" graph again to find what is similar to "Cat."

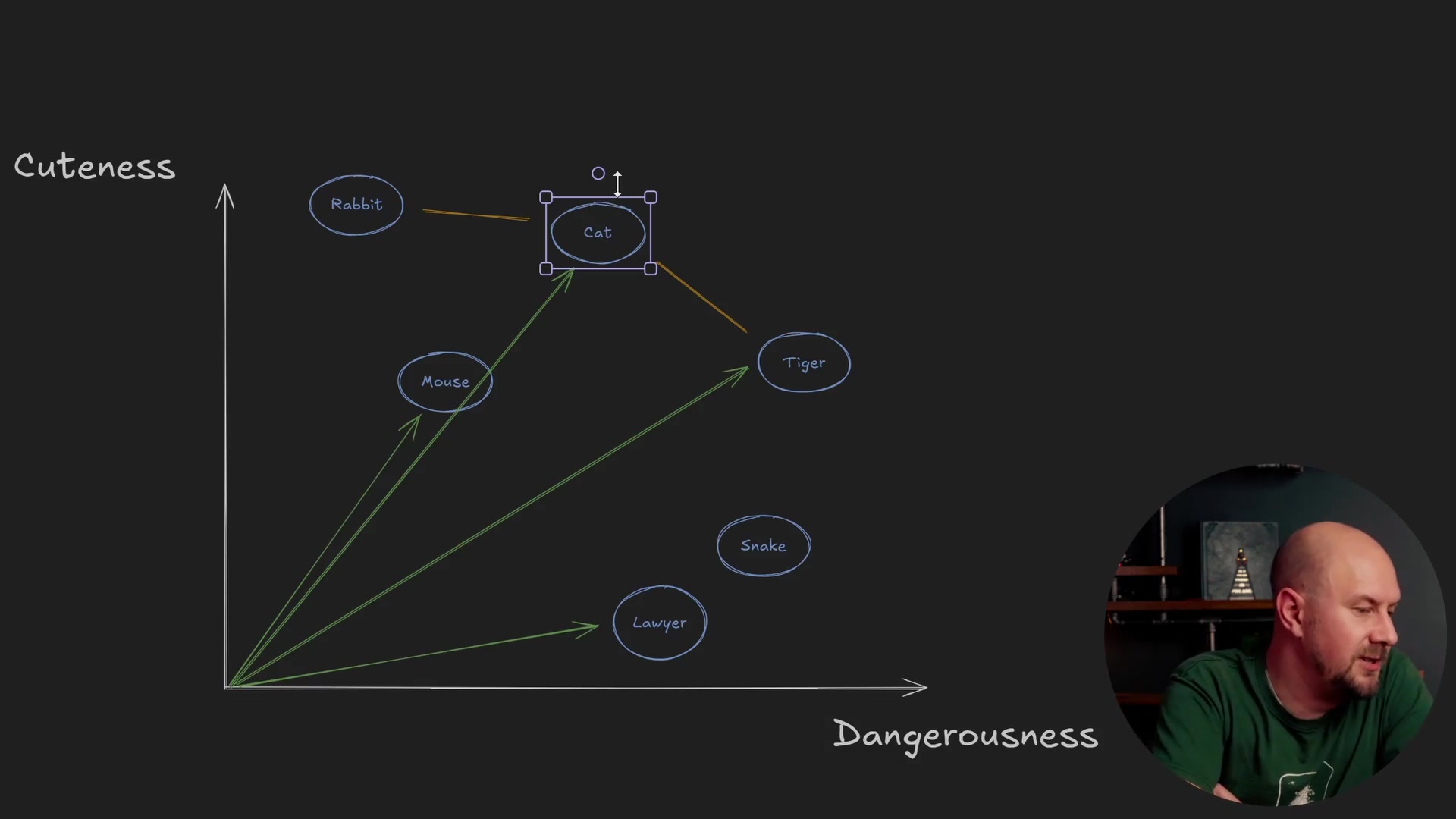
If we choose Euclidean distance:

• The closest items to "Cat" are "Rabbit" and "Tiger."
• We would say these two are the most similar because they have the shortest physical distance on the graph.
• "Cat" is a long way away from "Snake" and fairly far from "Mouse."

However, if we look at the Cosine similarity (represented by the green arrows):

• The map would say that "Cat" and "Mouse" are very similar.
• This is because they share a nearly identical angle from the origin.

Depending on which of these approaches you use, you will get significantly different search results.

Why Cosine Similarity is Usually Better for AI

By and large, cosine similarity is more popular when working with large language model embeddings. In this context, we will be using cosine similarity.

The reason for this popularity is how these models scale to multi-dimensional space. The direction down that multi-dimensional space is usually a lot more important than where the words are located absolutely in that space.

The "Happy" vs. "Ecstatic" Example

Here is another example to illustrate why direction matters more than distance. Let's look at three words: Happy, Calm, and Ecstatic. We will plot them on a graph where the Y-axis is "Positivity" and the X-axis is "Energy."

1. Happy: Plotted in the middle. It is quite positive and has quite high energy.
2. Calm: Also quite positive, but has low energy.
3. Ecstatic: Like "Happy," but just more of everything. It is super positive and super high energy.

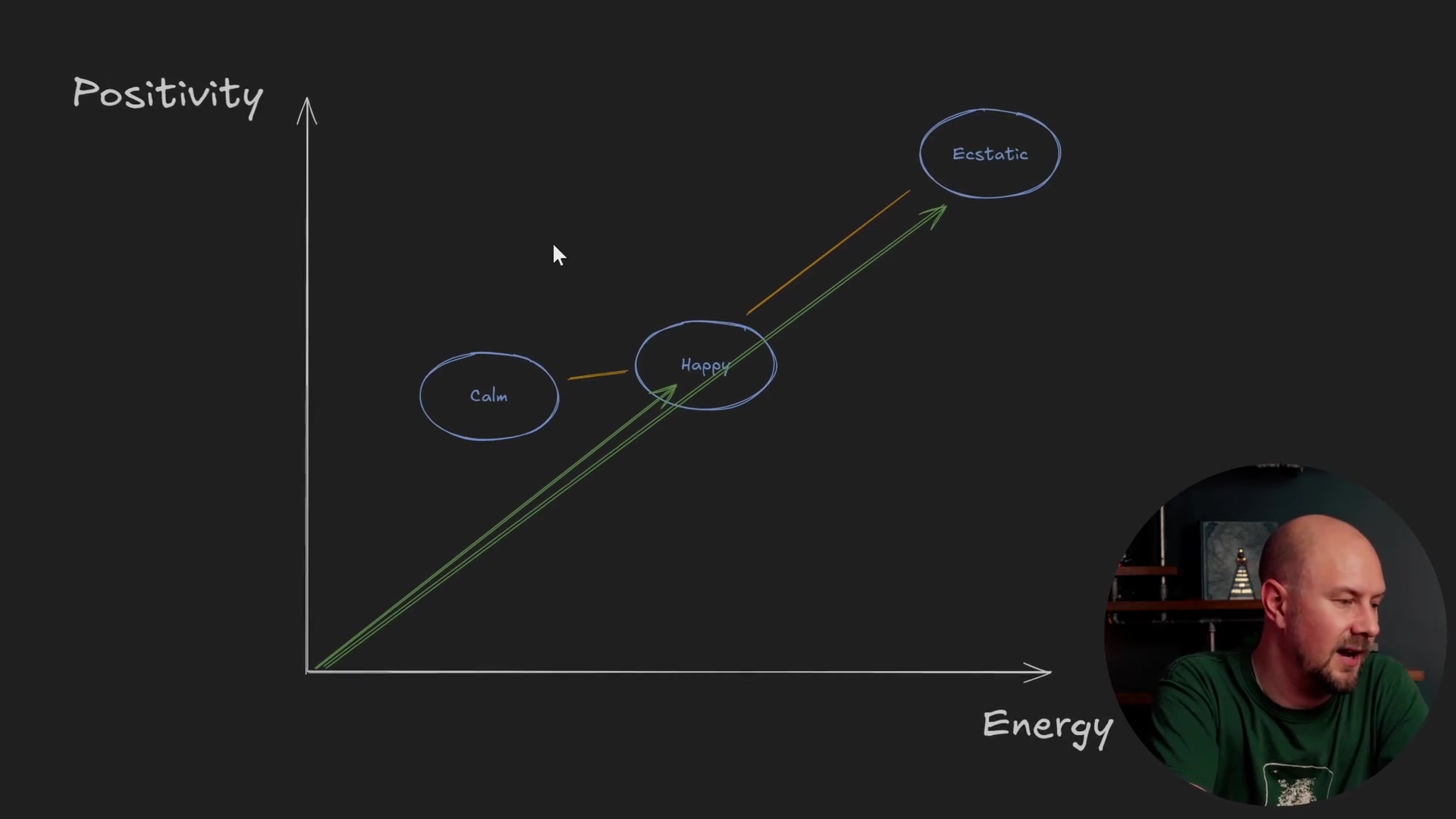
Now, if we wanted to find out what the closest adjective was to the word "Happy," let's see what happens with our two methods.

Using Euclidean Distance: If we used Euclidean distance, we would likely get the word "Calm." Why? because "Calm" is essentially "Happy" with less energy. It is physically closer on the graph. "Ecstatic" is much further away because the magnitude of the vector is so much larger.

Using Cosine Similarity: Look at the cosine similarity between these two. "Ecstatic" is essentially in the exact same direction as "Happy." It is just further along down that vector. "Ecstatic" and "Happy" have very, very similar vector directions.

Consequently, cosine similarity will bring "Ecstatic" out on top. If you take the word "Happy" and want to work out which word is closest to it, cosine similarity gives you "Ecstatic," while Euclidean distance gives you "Calm."

The Verdict on Meaning

I would argue that if you wanted to genuinely find the closest word to "Happy" out of these two options, "Ecstatic" is probably the word you are looking for.

Even though "Ecstatic" is more extreme (more positive, higher energy), they both share the same fundamental meaning. Remember, semantic search is all about meaning.

In a vector graph, the cosine similarity (the angle of the arrow) genuinely tells you what the meaning is. It tells you which direction in multi-dimensional space that word exists in. Euclidean distance is often rather arbitrary regarding semantic meaning because it is heavily influenced by the magnitude (or intensity) of the vector rather than its definition.

Ultimately, cosine similarity finds vectors that are in the same direction and therefore have the same meaning, even if those vectors did not end up in exactly the same position on the graph.

Recap

• Euclidean Distance measures the straight-line distance between two points on a graph. It focuses on absolute position.
• Cosine Similarity measures the angle between two vectors originating from the origin. It focuses on direction.
• In the context of semantic search and embeddings, direction equals meaning.
• We generally prefer Cosine Similarity because it identifies words with similar meanings (like "Happy" and "Ecstatic") even if their magnitudes (intensity) differ.